APP-Notes

• Types
  • Data types
    • Type synonyms
    • Algebraic Data Types
  • Destruction (💣)
    • Case
    • Wildcards
  • Records
  • Geparameterizeerde types
  • Binary search tree

Dag 5 - Types & Binary tree

Data types

Nieuwe types worden gedefinieerd met het data keyword. Om een type ‘BookInfo’ te definieren, kunnen we het volgende opschrijven:

data BookInfo = Book Int String [String]
                deriving (Show)

Het type bestaat uit de volgende dingen:

• BookInfo is de naam van het type. Deze start altijd met een hoofdletter. Deze wordt een ‘type constructor’ genoemd.
• Book wordt de value constructor of data constructor genoemd. Deze moet ook met een hoofdletter beginnen en wordt gebruikt om een value van het BookInfo type te maken.
• Int String [String] zijn de componenten van het type. Deze zijn vergelijkbaar met fields in Java. In het voorbeeld betekenen deze waardes het volgende:
  • Int: Het id van het boek
  • String: De titel van het boek
  • [String]: De auteurs van het boek

Dit type zou ook gedefinieerd kunnen worden als een tuple ((Int, String, [String])). Nu we een expliciet type gedefinieerd hebben hiervoor, kunnen we niet per ongeluk een tuple met deze waardes op de plaats van het BookInfo type meegeven. Er moet expliciet via de constructor van BookInfo een object aangemaakt worden.

Als we de repl tool gebruiken om wat info over dit type te vinden, komen de volgende dingen tevoorschijn:

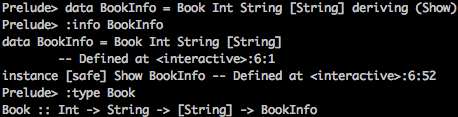
Er is te zien dat de constructor (Book) een functie is. Deze functie kan als volgt gebruikt worden om een nieuwe instantie van het type BookInfo aan te maken

boek = Book 91258654 "pietje puk en het grote geheim" ["Henri Arnoldus", "Henk Smit"]

Dit BookInfo type zou in Java opgeschreven worden als:

public class BookInfo {
    public int Id;
    public String Title;
    public String[] Authors;
}

Type synonyms

Type synonyms doen wat de naam zegt. Deze bieden synoniemen voor bestaande types. De reden dat dit gewenst zou zijn, is om meer duidelijkheid te geven waar een type voor gebruikt wordt. Een voorbeeld is het synonym ‘ISBN’. Deze kan vervolgens weer gebruikt worden in het BookInfo type: type ISBN = String.

Algebraic Data Types

Algebraic data types zijn types die meer dan 1 value constructor hebben. De Bool is hier het simpelste voorbeeld van. Deze heeft de value constructors True en False. Een ander voorbeeld is het in rekening brengen van kosten. Hiervoor kan een BillingInfo type geintroduceerd worden:

data BillingInfo
    = CreditCard CardNumber CardHolder Address
    | CashOnDelivery
    | Invoice CustomerId
      deriving (Show)

Hiermee specificeren we dat er op verschillende manieren betaald kan worden. Namelijk met Credit card, in cash bij aflevering of per factuur. Via pattern matching kan er vervolgens gekeken worden welke BillingInfo er gebruikt wordt. Zowel de CreditCard, CashOnDelivery als de Invoice zijn in dit voorbeeld value constructors.

Destruction (💣)

Om iets met de hierbovengenoemde types te kunnen, kunnen we pattern matching toepassen. We willen namelijk, in het geval van een type met meerdere value constructors, weten welke value constructor gebruikt wordt. Ook willen we waardes uit de gebruikte value constructor halen.

Het aanmaken van instanties van types noemen we constructing. Het vervolgens uit elkaar halen van een instantie noemen we destructing. Dit werkt als volgt:

module BookInfo(readBookInfo) where
import Data.List (intercalate)

data BookInfo = Book Int String [String]
                deriving (Show)

readBookInfo :: BookInfo -> String
readBookInfo (Book isbn title authors) =
    "ISBN: " ++ show isbn ++
    " Title: " ++ title ++
    " Authors: " ++ intercalate "," authors

Via de constructor wordt het type zowel in elkaar gezet als weer uit elkaar gehaald.

Case

In talen als Java kennen we de Enum. Wanneer er voor een algebraic data type alleen value constructors gespecificeerd worden zonder parameters, lijken deze verdacht veel op Enums.

public enum BillingInfo {
    CreditCard,
    CashOnDelivery,
    Invoice
}

In Java zullen we al snel op subclasses terecht komen. Dit zou er bijvoorbeeld uitzien als:

public interface BillingInfo {
}

public class CreditCard implements BillingInfo {
    public int CardNumber;
    public String CardHolder;
    public String Address;
}

public class CashOnDelivery implements BillingInfo {
}

public class Invoice implements BillingInfo {
    public int CustomerId;
}

// Een random punt ergens in een random class
// Dit kan ook opgelost worden door bijvoorbeeld de data die teruggegeven
// wordt in sendOrder in de toString functies van de 3 types te stoppen.
// Het gaat echter om het principe dat er data uit het BillingInfo type gehaald
// wordt, zodat deze ergens in een functie gebruikt kan worden om bijvoorbeeld
// een bestelling af te handelen.
public String sendOrder (BillingInfo billingInfo) {
    if (billingInfo instanceOf CreditCard) {
        CreditCard creditCard = (CreditCard)billingInfo;
        return
            "Chose payment by credit card: " +
            " Card number: " + creditCard.CardNumber +
            " Card holder: " + creditCard.CardHolder;
    }
    else if (billingInfo instanceOf CashOnDelivery) {
        return "Chose cash on delivery";
    }
    else if (billingInfo instanceOf Invoice) {
        Invoice invoice = (Invoice)billingInfo;
        return "Chose payment by invoice for customer: " + invoice.CustomerId;
    }
    else {
        throw new UnsupportedOperationException();
    }
}

In Haskell kan dit op verschillende manieren gedaan worden. Een manier is de case statement:

module Payment(sendOrder) where

type CardNumber = Int
type CardHolder = String
type Address = String
type CustomerId = Int

data BillingInfo
    = CreditCard CardNumber CardHolder Address
    | CashOnDelivery
    | Invoice CustomerId
      deriving (Show)

sendOrder :: BillingInfo -> String
sendOrder billingInfo =
    case billingInfo of
        CreditCard cardNum cardHolder address ->
            "Chose payment by credit card: " ++
            " Card number: " ++ show cardNum ++
            " Card holder: " ++ cardHolder ++ address

        CashOnDelivery ->
            "Chose cash on delivery"

        Invoice customerId ->
            "Chose payment by invoice for customer: " ++ show customerId

en de andere manier is via pattern matching:

sendOrder :: BillingInfo -> String
sendOrder (CreditCard cardNum cardHolder address) =
    "Chose payment by credit card: " ++
    " Card number: " ++ show cardNum ++
    " Card holder: " ++ cardHolder ++ address
sendOrder CashOnDelivery = "Chose cash on delivery"
sendOrder (Invoice customerId) = "Chose payment by invoice for customer: " ++ show customerId

Wildcards

Wanneer we enkel geinteresseerd zouden zijn in bijvoorbeeld de titel van een boek, kunnen we wildcards gebruiken om de overige waardes te negeren. Deze komen in de vorm van een _. Dit ziet er als volgt uit:

readTitle :: BookInfo -> String
readTitle (Book _ title _) =
    "Title: " ++ title

Een andere situatie waar we wildcards kunnen gebruiken, is bij het pattern matchen op type constructors. Wanneer we bijvoorbeeld specifiek bij de CashOnDelivery value constructor iets willen doen en bij de overige value constructors iets anders, kunnen we dit als volgt noteren:

sendOrder :: BillingInfo -> String
sendOrder CashOnDelivery = "Cash on delivery"
sendOrder _ = "Some other way of paying"

Records

Om componenten uit de data types te halen, moeten we getters specificeren. Een ander woord hiervoor is boilerplate en daar houdt niemand van. Om deze boilerplate te voorkomen kent Haskell het concept van een Record. Records zijn gewone datatypes, waarbij er per component een getter functie wordt gegenereerd. Deze getter functie draagt dezelfde naam als die van het component. Dit ziet er als volgt uit:

data Customer = Customer
    { customerId :: Int
    , customerName :: String 
    , customerAddress :: String
    }

printCustomer :: Customer -> String
printCustomer customer =
    "Id: " ++ show (customerId customer) ++
    " Name: " ++ customerName customer ++
    " Address: " ++ customerAddress customer

Ook kunnen records gebruikt worden in algebraic data types. Dit werkt precies hetzelfde als dat toegelicht is.

data Customer 
    = AwesomeCustomer
        { customerId :: Int
        , customerName :: String 
        , customerAddress :: String
        }
    | SomethingElse
    | AnotherSomethingElse

Geparameterizeerde types

Types kunnen ook een parameter meekrijgen. Een mooi voorbeeld hiervan is het Maybe type. Het maybe type heeft 2 waardes. Just en Nothing:

data Maybe a
    = Just a
    | Nothing

Het type a kan vanalles zijn. Het gebruik van een maybe in een functie ziet er als volgt uit:

doFoo :: Maybe Int -> String
doFoo maybeNumber =
    ...

In dit codevoorbeeld specificeren we dat de Maybe een ding bevat van het type Int. Hier kan vervolgens via pattern matching weer een waarde tevoorschijn getoverd worden.

Binary search tree

Voor de binaire zoek boom heb ik besloten een boom met de volgende functies te schrijven:

• add (zonder AVL)
• contains
• toArray

Als eerste ben ik begonnen met het opzetten van de structuur. Voor de node elementen heb ik een algebraic data type gebruikt. Dit type kan zowel leeg zijn als een value hebben.

data BinaryTreeNode a
    = EmptyNode
    | ValueNode a (BinaryTreeNode a) (BinaryTreeNode a)
    deriving (Show)

Vervolgens heb ik een add functie gedefinieerd. Omdat dit een recursieve functie betreft, heb ik als eerst een base case gemaakt. Dit is het geval van een EmptyNode. Wanneer deze als input dient, kan er simpelweg een nieuwe ValueNode aangemaakt worden met hierin de opgegeven value.

Als tweede case heb ik de ValueNode opgenomen. Vanaf hier is het simpelweg een kwestie van de boom aflopen tot ik een lege node tegenkom.

add :: Ord a => a -> BinaryTreeNode a -> BinaryTreeNode a
add newVal EmptyNode = ValueNode newVal EmptyNode EmptyNode
add newVal (ValueNode existingVal left right)
    | newVal < existingVal = ValueNode existingVal (add newVal left) right
    | newVal > existingVal = ValueNode existingVal left (add newVal right)
    | otherwise            = ValueNode existingVal left right

Omdat het BinaryTreeNode type derived van Show, heeft deze de show functie tot zijn beschikking. De show functie is vergelijkbaar met de toString functie in talen als Java of C#. By-default loopt deze methode het algebraic datatype al recursief af, dus hier hoeft geen aparte functie voor geschreven te worden.

Nu we dingen toe kunnen voegen en af kunnen drukken, is het tijd om de contains functie te schrijven. Ook dit is een kwestie van het recursief aflopen van de boom. Omdat het voor een binary tree essentieel is dat er volgorde in de waardes zit die in de boom gestopt kunnen worden, heb ik bij alle functies de eis toegevoegd dat de waardes die in de boom zitten sorteerbaar zijn doordat ze van Ord erven. Voor het zoeken door de boom heb ik gebruik gemaakt van guards. Hier zijn de EmptyNode en de value == existingVal de base cases.

contains :: Ord a => a -> BinaryTreeNode a -> Bool
contains value EmptyNode = False
contains value (ValueNode existingVal left right)
    | value == existingVal = True
    | value < existingVal  = (contains value left)
    | otherwise            = (contains value right)

Het afdrukken van de boom in een array heb ik gedaan door steeds de toArray van de linkerhelft samen te voegen met de huidige value en daarna de rechter helft. Hiervoor heb ik gebruik gemaakt van de infix-functies ++ en :. ++ heeft als type signature ++ :: [a] -> [a] -> [a]. : heeft als type signature : :: a -> [a] -> [a].

toArray :: Ord a => BinaryTreeNode a -> [a]
toArray EmptyNode = []
toArray (ValueNode value left right) =
    (toArray left) ++ value : (toArray right)

Nog even het totaalplaatje:

module BinaryTree(add, contains, toArray) where

data BinaryTreeNode a
    = EmptyNode
    | ValueNode a (BinaryTreeNode a) (BinaryTreeNode a)
    deriving (Show)

add :: Ord a => a -> BinaryTreeNode a -> BinaryTreeNode a
add newVal EmptyNode = ValueNode newVal EmptyNode EmptyNode
add newVal (ValueNode existingVal left right)
    | newVal < existingVal = ValueNode existingVal (add newVal left) right
    | newVal > existingVal = ValueNode existingVal left (add newVal right)
    | otherwise            = ValueNode existingVal left right

contains :: Ord a => a -> BinaryTreeNode a -> Bool
contains value EmptyNode = False
contains value (ValueNode existingVal left right)
    | value == existingVal = True
    | value < existingVal  = (contains value left)
    | otherwise            = (contains value right)

toArray :: Ord a => BinaryTreeNode a -> [a]
toArray EmptyNode = []
toArray (ValueNode value left right) =
    toArray left ++ value : toArray right