APP-Notes
Dag 7 - AVL boom
Omdat ik nu aardig wat geexpirimenteerd heb met Haskell, wordt het tijd om wat te puzzelen. Op dag 6 heb ik een binaire zoekboom gemaakt die nog geen AVL ondersteunde. Vandaag ga ik deze de mogelijkheid geven om zichzelf bij het toevoegen AVL te maken, wanneer het toevoegen ervoor zorgt dat de boom niet meer gebalanceerd is.
Diepte en AVL detectie
Als eerste wil ik kunnen detecteren of de (sub)boom gebalanceerd is. De boom is gebalanceerd wanneer de diepte van links gelijk is, of 1 groter/kleiner is dan rechts. Wanneer dit verschil groter dan 1 is, is de boom niet AVL. Ik wil dus eerst kunnen zien wat de diepte van een boom is. De diepte wordt berekend door de de grootste van de linker en rechter diepte te nemen en hier 1 bij op te tellen. Doe dit recursief tot je bij de EmptyNode bent en je hebt de diepte van de boom.
depth :: Ord a => BinaryTreeNode a -> Integer
depth EmptyNode = 0
depth (ValueNode _ left right) =
1 + max (depth left) (depth right)
Nu we de diepte kunnen berekenen, kunnen we kijken of de boom AVL is. Hiervoor is de abs functie nuttig. Door de rechter diepte van de linker diepte af te trekken, krijgen we een verschil terug. Als links echter kleiner is dan rechts, is deze waarde negatief. Hier gebruik ik de abs functie voor. Deze functie pakt de absolute waarde van een gegeven getal. Een negatieve waarde wordt dus positief.
isAvl :: Ord a => BinaryTreeNode a -> Bool
isAvl EmptyNode = True
isAvl (ValueNode _ left right) =
abs (depth left - depth right) < 2
Rotaties
Aan de hand van deze wikipedia afbeelding is te zien hoe bomen in verschillende situaties gebalanceerd kunnen worden. Er zijn dubbele en enkele rotaties. De enkele rotaties zijn het gemakkelijkste. Eerst haal ik de benodigde nodes uit elkaar met behulp van pattern matching. Dit ziet er ingewikkeld uit, maar is het niet. Het is een kwestie van goed kijken en even doorhebben wat er gebeurt. Nu de benodigde nodes uit elkaar zijn gehaald, kan ik ze in de juiste volgorde weer in elkaar zetten.
rotateRight :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateRight (ValueNode rootVal (ValueNode lVal lLeftTree lRightTree) rootRightTree) =
ValueNode
lVal
lLeftTree
(ValueNode
rootVal
lRightTree
rootRightTree)
rotateLeft :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateLeft (ValueNode rootVal rootLeftTree (ValueNode rVal rLeftTree rRightTree)) =
ValueNode
rVal
(ValueNode
rootVal
rootLeftTree
rLeftTree)
rRightTree
De dubbele rotaties zijn niets anders dan twee keer een enkele rotatie op verschillende niveaus. Voor de dubbele rotaties kunnen we deze functies dus hergebruiken.
rotateLeftRight :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateLeftRight (ValueNode rootVal left right) =
rotateRight (ValueNode rootVal (rotateLeft left) right)
rotateRightLeft :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateRightLeft (ValueNode rootVal left right) =
rotateLeft (ValueNode rootVal left (rotateRight right))
We kunnen detecteren of een boom AVL is en we kunnen rotaties uitvoeren. Echter kunnen we in de add functie nog niet detecteren op welke manier er geroteerd moet worden. Hiervoor is het handig om een trace bij te houden. Een nieuwe node legt bij het toevoegen een reis af door de boom. Steeds kiest die voor links of voor rechts. In het wikipedia voorbeeld zouden dit de volgende traces zijn:
- Left Left Case:
Links, Links - Right Right Case:
Rechts, Rechts - Left Right Case:
Links, Rechts - Right Left Case:
Rechts, Links
Voor deze trace zijn enkel de laatste 2 stappen van belang voor het roteren. Voor het AVL maken, heb ik de makeAvl functie gemaakt. Deze functie gebruikt het nieuwe data type Side. Omdat de value constructors Left en Right al bezet zijn door een andere library (Prelude), heb ik voor AddLeft en AddRight gekozen.
data Side
= AddLeft
| AddRight
makeAvl :: Ord a => BinaryTreeNode a -> [Side] -> BinaryTreeNode a
makeAvl tree [AddLeft, AddLeft] = rotateRight tree
makeAvl tree [AddRight, AddRight] = rotateLeft tree
makeAvl tree [AddLeft, AddRight] = rotateLeftRight tree
makeAvl tree [AddRight, AddLeft] = rotateRightLeft tree
Nieuwe insert functie
De trace kan recursief opgebouwd worden. Om de add niet van interface te laten veranderen, heb ik een insert functie toegevoegd. Deze functie is private en geeft bij het toevoegen van een node de nieuwe boom en een trace terug. Deze functie kijkt steeds, met behulp van een case statement, aan welke kant de node toegevoegd moet worden. Vervolgens wordt de nieuwe boom aangemaakt en wordt vervolgens het pad geupdate.
Na het updaten van het pad moet er nog gekeken of de boom AVL is. Hiervoor staat het eerste gedeelte in een let statement. Dit maakt het mogelijk om een tijdelijke variabele te declareren.
insert :: Ord a => a -> BinaryTreeNode a -> (BinaryTreeNode a, [Side])
insert newVal EmptyNode = (ValueNode newVal EmptyNode EmptyNode, [])
insert newVal (ValueNode existingVal left right) =
let
(tree, trace) =
case compare newVal existingVal of
LT ->
let (newLeft, leftTrace) = insert newVal left
in (ValueNode existingVal newLeft right, [AddLeft] ++ leftTrace)
GT ->
let (newRight, rightTrace) = insert newVal right
in (ValueNode existingVal left newRight, [AddRight] ++ rightTrace)
EQ -> (ValueNode existingVal left right, [])
in
if (isAvl tree) then (tree, trace)
else (makeAvl tree trace, trace)
De add functie moet nu alleen nog aangepast worden om de nieuwe insert functie te gebruiken. Omdat we de trace niet nodig hebben, gebruik ik hier een _.
add :: Ord a => a -> BinaryTreeNode a -> BinaryTreeNode a
add newVal tree =
let
(newTree, _) =
insert newVal tree
in
newTree
Het totaalplaatje
Met name de insert functie vereisde veel nadenkwerk. Hier komt zowel een voordeel als nadeel van Haskell erg naar boven. Het is lastig om tijdelijke variabelen te zetten, omdat er dan met let in statements gespeeld moet worden. Echter zorgt dit er wel voor dat er vroegtijdig goed nagedacht wordt over de code. Tijdens het maken van de code voelde ik mij soms erg gelimiteerd in de manier van werken, maar toen het eenmaal werkte stond er een vrij elegant stuk code (en ja, dit kostte aardig wat tijd).
Het totaalplaatje van de boom is nu als volgt:
module BinaryTree(add, contains, toArray, depth) where
data BinaryTreeNode a
= EmptyNode
| ValueNode a (BinaryTreeNode a) (BinaryTreeNode a)
deriving (Show)
data Side
= AddLeft
| AddRight
contains :: Ord a => a -> BinaryTreeNode a -> Bool
contains _ EmptyNode = False
contains value (ValueNode existingVal left right)
| value == existingVal = True
| value < existingVal = (contains value left)
| otherwise = (contains value right)
toArray :: Ord a => BinaryTreeNode a -> [a]
toArray EmptyNode = []
toArray (ValueNode value left right) =
toArray left ++ value : toArray right
depth :: Ord a => BinaryTreeNode a -> Integer
depth EmptyNode = 0
depth (ValueNode _ left right) =
1 + max (depth left) (depth right)
add :: Ord a => a -> BinaryTreeNode a -> BinaryTreeNode a
add newVal tree =
let
(newTree, _) =
insert newVal tree
in
newTree
insert :: Ord a => a -> BinaryTreeNode a -> (BinaryTreeNode a, [Side])
insert newVal EmptyNode = (ValueNode newVal EmptyNode EmptyNode, [])
insert newVal (ValueNode existingVal left right) =
let
(tree, trace) =
case compare newVal existingVal of
LT ->
let (newLeft, leftTrace) = insert newVal left
in (ValueNode existingVal newLeft right, [AddLeft] ++ leftTrace)
GT ->
let (newRight, rightTrace) = insert newVal right
in (ValueNode existingVal left newRight, [AddRight] ++ rightTrace)
EQ -> (ValueNode existingVal left right, [])
in
if (isAvl tree) then (tree, trace)
else (makeAvl tree trace, trace)
isAvl :: Ord a => BinaryTreeNode a -> Bool
isAvl EmptyNode = True
isAvl (ValueNode _ left right) =
abs (depth left - depth right) < 2
makeAvl :: Ord a => BinaryTreeNode a -> [Side] -> BinaryTreeNode a
makeAvl tree [AddLeft, AddLeft] = rotateRight tree
makeAvl tree [AddRight, AddRight] = rotateLeft tree
makeAvl tree [AddLeft, AddRight] = rotateLeftRight tree
makeAvl tree [AddRight, AddLeft] = rotateRightLeft tree
rotateLeftRight :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateLeftRight (ValueNode rootVal left right) =
rotateRight (ValueNode rootVal (rotateLeft left) right)
rotateRightLeft :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateRightLeft (ValueNode rootVal left right) =
rotateLeft (ValueNode rootVal left (rotateRight right))
rotateRight :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateRight (ValueNode rootVal (ValueNode lVal lLeftTree lRightTree) rootRightTree) =
ValueNode
lVal
lLeftTree
(ValueNode
rootVal
lRightTree
rootRightTree)
rotateLeft :: Ord a => BinaryTreeNode a -> BinaryTreeNode a
rotateLeft (ValueNode rootVal rootLeftTree (ValueNode rVal rLeftTree rRightTree)) =
ValueNode
rVal
(ValueNode
rootVal
rootLeftTree
rLeftTree)
rRightTree
Door wat testcases te maken, kunnen we zien dat het werkt zoals het zou moeten werken
Left Left Case
De verwachtte output:
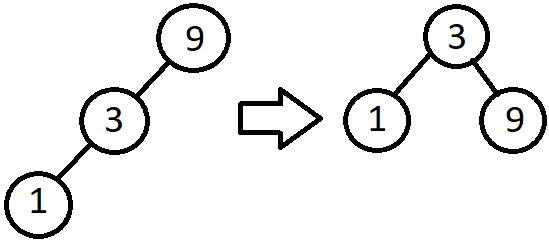
De gekregen output:

Right Right Case
De verwachtte output:
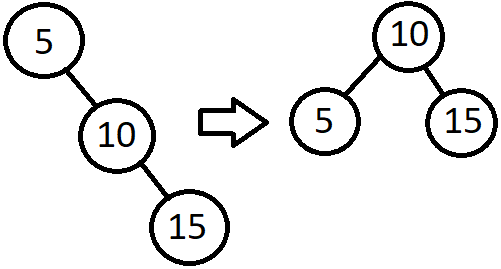
De gekregen output:

Left Right Case
De verwachtte output:
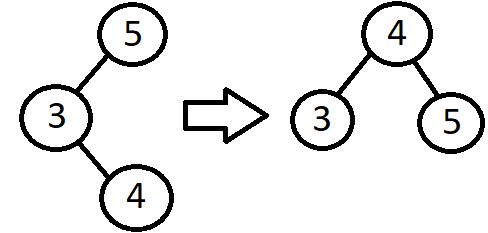
De gekregen output:

Right Left Case
De verwachtte output:
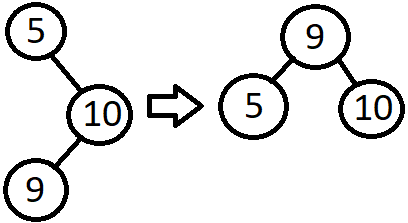
De gekregen output:
